Tipos de resolución
Una de las utilidades básicas de la Hoja de Cálculo en la Enseñanza es ayudar a adquirir hábitos de orden y claridad en la resolución de problemas. Con su uso se facilita: el recuento de variables que intervienen en un problema, las fórmulas necesarias y las rutas de resolución existentes entre ellas. Sólo en este sentido, de manejar fórmulas y variables, usaremos (en esta sesión) la palabra resolución, que evidentemente tiene un significado mucho más amplio.
Estos modelos pueden construirse para realizar tres tareas distintas:Modelos de resolución
Resumen toda una batería de fórmulas (ámbito de fórmulas) que se usan en un tema científico determinado (por ejemplo el de los elementos de un triángulo rectángulo) mediante la consideración separada de variables (hipotenusa, catetos, ángulos...) y de fórmulas (teorema de Pitágoras, suma de ángulos, razones trigonométricas...). Nuestro objetivo es resolver todos los problemas de tipo algebraico que se pueden plantear en ese ámbito de variables y fórmulas.
Todas las Ciencias están llenas de ámbitos de fórmulas. Damos algún ejemplo:
- Ecuaciones de los gases perfectos
- Dinámica del plano inclinado
- Disoluciones
- Movimiento armónico simple
- Corriente alterna
- Amortización de un préstamo
Un concepto próximo a éste es el de “Caja de herramientas”, en el que además de las herramientas algebraicas se pueden añadir párrafos de teoría, distintos módulos de resolución, funciones definidas, etc.
Análisis de situaciones
Consisten en reflejar en una Hoja los elementos de una situación concreta en un ámbito científico, por ejemplo: la comparación entre la posición inicial de un péndulo y la velocidad con la que pasa por su punto de equilibrio. En este caso recurriríamos también a una colección de fórmulas y variables, así como a tablas que las relacionen, pero no la totalidad del ámbito, sino sólo las que nos interesen en esa situación determinada. En el ejemplo anterior no consideraríamos el periodo del péndulo.Rutas de resolución
Esta tarea es similar a la anterior, pero resumiendo una resolución de problemas en un organigrama que nos lleve desde los datos a la solución del mismo.
En la imagen puedes ver una ruta en forma de organigrama para calcular el calor desprendido por una resistencia dada cuando se conecta a una diferencia de potencial. Como ves, es una forma muy intuitiva para resumir un planteo de problema, con la ventaja de poder cambiar los datos a voluntad y experimentar con ellos.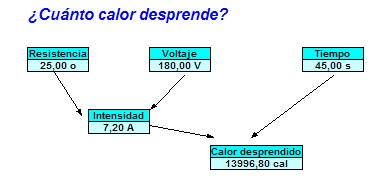
Puedes consultar el modelo que contiene este organigrama en orga1.ods, de la carpeta Modelos. En él descubrirás las fórmulas usadas para el cálculo de la intensidad y el calor.
