Práctica: Estudio de una situación concreta
La Hoja de Cálculo permite estudiar toda situación de tipo matemático o de las Ciencias Experimentales que se pueda expresar mediante variables y fórmulas. Como práctica de esta sesión construirás un modelo que estudie la siguiente situación:
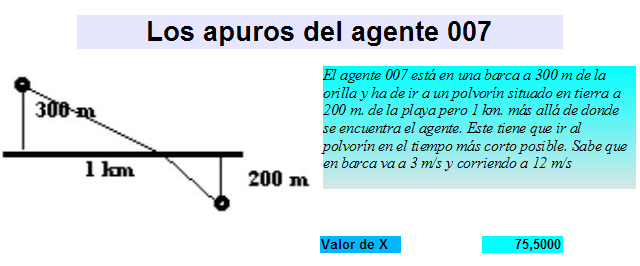
El agente 007 está en una barca a 300 m de la orilla y ha de ir a un polvorín situado en tierra a 200 m. de la playa pero 1 km. más allá de donde se encuentra el agente. Este tiene que ir al polvorín en el tiempo más corto posible. Sabe que en barca va a 3 m/s y corriendo a 12 m/s
a) ¿A qué punto de la playa debe ir para tardar el menor tiempo posible?
b) ¿Qué distancia ha recorrido?
c) ¿Se cumple aquí una ley parecida a la de la luz cuando cambia de medio (aire a cristal, por ejemplo) en la que sen(a1)/sen(a2) = v1/v2 ?
d) ¿En qué trayecto el tiempo en el agua es el doble que el de tierra?
Para estudiar una situación debemos, en primer lugar, decidir qué variables estudiaremos sobre ella. También puede ser conveniente clasificarlas en básicas y complementarias.
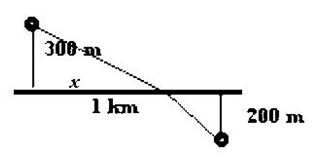
En este caso la variable fundamental, de la que dependen las demás es la distancia x medida en la costa entre la perpendicular desde la barca y el punto de la orilla al que se dirige el agente.
Comenzaremos, pues, el modelo destacando esa variable. Para practicar lo que has aprendido en esta sesión puedes incluir un título con la Galería de Fontwork (o bien en una celda grande con colores de fondo y bordes) y un resumen de la situación en un cuadro de texto. Ambos objetos los puedes insertar con la Barra de Dibujo, que ya has visto al principio de la sesión.
Para insertar un cuadro de texto comienzas también con esa Barra de Dibujo y eliges el botón de la T, el de Texto, como ya viste en la sesión 4. Recuerda que si lo señalas con el ratón:
- una doble pulsación te abre opciones de texto
- una pulsación simple permite modificar aspectos de dibujo
Pulsa, pues, una vez y elige Formato > Gráfico > Relleno > Gradientes, o la Barra de Formatos, para dotar al cuadro de un gradiente de color. Puede quedar así:

También puedes insertar el gráfico de la situación, que lo puedes copiar de este mismo documento que estás leyendo.
La cabecera del modelo puede ser similar a esta.
Es importante que destaques la variable principal: Valor de x
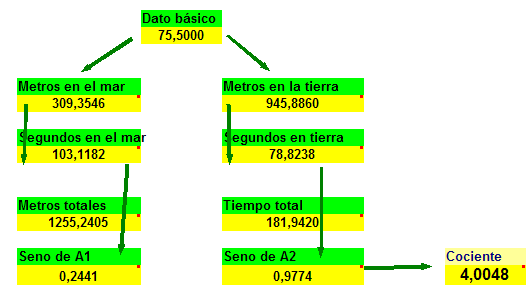
El resto del modelo contendrá los cálculos necesarios hasta llegar a la comprobación de que el cociente de los senos de los dos ángulos coincide con el inverso del cociente de velocidades, que en este caso es de 4. En la figura se incluye una disposición de cálculos y los resultados para el valor x=75,5 m que es el que da el tiempo mínimo de 181,94 s y se responde, por tanto, a las cuestiones a) a c).

Los metros en tierra y en mar resultan de la aplicación del Teorema de Pitágoras y los segundos del cociente entre los metros y las velocidades. Los senos de los ángulos se calculan a partir de su definición.
Si tienes alguna duda en la construcción del modelo consulta agente007.ods.
Una idea interesante es la de usar la Búsqueda de valor destino para obligar a que el cociente de los senos sea 4, equivalente al de velocidades, con lo que obtendrás el tiempo mínimo. Los datos serían Celda de la fórmula: la que contenga el valor del cociente, Valor destino: 4, Celda variable: la que contiene el valor de X. Así obtendríamos un tiempo de 181,94 para un valor de X de 75,6 m.
Esta situación se podía haber resumido en un organigrama que representara la ruta de resolución. En la hoja 2 del modelo agente007.ods se ha incluido uno con notas en cada celda importante, a fin de que quien lo consulte pueda saber en qué fórmula o Teorema se basa cada cálculo. También puedes leer las fórmulas incluidas y comprobar que contienen copias dinámicas entre hojas mediante el uso del signo =.
Puedes ampliar el modelo incluyendo como variables básicas las distancias y velocidades. También es conveniente que resuelvas la cuestión d), cuya solución es x=247,85 m. Puedes encontrar la solución por tanteo. Te ayudaría incluir en una celda la fórmula =tiempo en agua – 2*tiempo en tierra.
Inventa otras cuestiones sobre esta situación.
Si deseas ver más ejemplos de situaciones que se han analizado en las clases de Bachillerato, consulta el documento situaciones.pdf.