Sistema de ecuaciones lineales
Con un poco de habilidad, la herramienta Solver puede resolver sistemas de ecuaciones lineales, con un máximo de cinco ecuaciones.
Imagina que deseas resolver este sistema
2X+Y+Z+W=10
4X+7Y+2U+2W=30
2X+Y-3Z-2U+W=-2
2X-Y+Z+U+2W=10
4X+Z+U+W=14
Bastará reflejar cuatro de las ecuaciones como restricciones, y la quinta como la celda a optimizar. Tanto en unas como en otra, deberemos usar el signo =
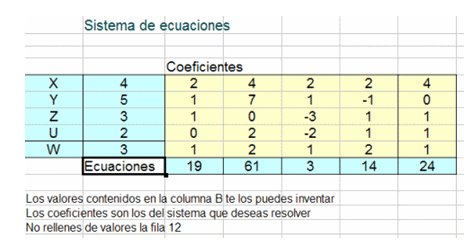
Abre la hoja siste1.ods, que ya está preparada para alojar una ecuación y tratarla con Solver.En la imagen ya están escritos los coeficientes y los valores de las incógnitas están elegidos aleatoriamente.
Sobre estos datos aplicamos Solver de la siguiente forma:
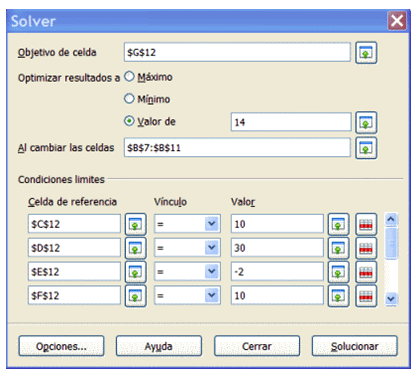
Las cuatro primeras ecuaciones están tratadas como restricciones. Observa las celdas $C$12 a $F$12 y los valores asignados: 10, 30, -2 y 10 que son los segundos miembros de esas ecuaciones.
La quinta ecuación se ha tratado como celda a optimizar con una asignación de valor de 14, que es el último término independiente.
El rango a cambiar es el que contiene los valores de las incógnitas.
Pulsa en Solucionar y obtendrás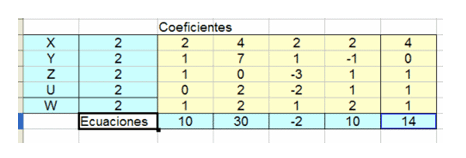
que es la solución del sistema: X=Y=Z=U=W=2
Si deseas resolver un sistema de menor número de ecuaciones, rellena con ceros y usa un menor número de restricciones.