Resolvedores
Con los modelos de una Hoja de Cálculo podemos verificar la antigua máxima de que un mismo problema se hace distinto si se usan para su resolución instrumentos distintos. Para comprobarlo usaremos una batería de cuestiones sobre resistencias en paralelo e iremos observando la adecuación de los modelos a la resolución de cada una. A estos modelos les llamaremos Resolvedores, palabra coloquial con la que queremos resaltar su capacidad de ayuda en la resolución de problemas.
Seguimos con el modelo paralelo.ods.
Con el módulo básico situado en la primera hoja sólo tienes tres opciones para calcular unas variables en función de otras:
- Cálculo directo sobre los datos dados
- Tanteo de valores hasta encontrar el que encaje con el resto de datos
- Uso de la técnica de Búsqueda de valor destino
Como ejemplo resuelve la cuestión 1 de la batería paralelo.pdf:
1 Dos resistencias de 6 Ω y 18 Ω respectivamente se conectan en paralelo bajo una diferencia de potencial de 20 V
(a) Si una resistencia, como ves, es el triple de la otra, ¿Se guarda la misma proporción en las intensidades que las atraviesan? ¿Y en la potencia consumida en cada una? Cambia la proporción al doble, por ejemplo a 6 Ω y 12 Ω ¿Ocurriría lo mismo?
Este sería un ejemplo de uso directo del módulo: escribimos los datos 6 Ω, 18 Ω y 20 V en los datos y obtenemos intensidades y potencias que guardan la misma proporción de 3 a 1. Cambiamos a otra proporción y vemos que se reproduce de forma inversa.
(b) ¿A qué diferencia de potencial han de someterse para que por la primera circulen 7 amperios? ¿Y para que la intensidad total sea de 4,2 A?
La primera solución la podemos encontrar por tanteo. Cambia los valores de la celda D27 del potencial hasta dar con el valor adecuado de 42 V, que es el que produce la intensidad 7 A.
La segunda se puede obtener por búsqueda de valor destino.
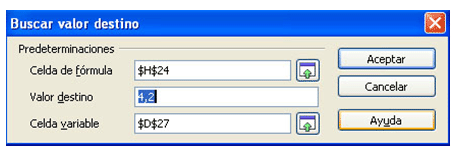
Basta dar los datos:
Celda de fórmula: $H$24 (la intensidad total)
Valor destino: 4,2
Celda variable: $D$27 (la diferencia de potencial) para obtener la solución de 18,9 V.
(c) En el primer apartado de la cuestión anterior cambia el dato de 18 Ω en la segunda resistencia por otro cualquiera. Observa las soluciones que obtienes. Saca una consecuencia.
Cambia el valor de la resistencia segunda en la celda D25 y observarás que no influye en el resultado de 7 A, suponiendo que el voltaje se mantiene constante.
Intenta obtener la solución de la segunda cuestión de la batería:
2 Las resistencias de la cuestión anterior han disipado en forma de calor 67.000 J conectadas a una fuente de 220 voltios ¿Cuánto tiempo han estado conectadas?
Como ejemplo final del uso de este módulo básico resolveremos la cuestión 3
3 Un cable constituye una resistencia de 2,8 Ω , y queremos cortarlo en dos trozos, no necesariamente iguales, y conectarlos en paralelo. ¿Cómo repartiríamos los trozos para conseguir una resistencia total de 0,66 Ω .?
Desprotege el modelo si aún no lo has hecho y escribe en una celda (por ejemplo la B35) la resistencia total 2,8. Como valor en la primera resistencia escribe un valor orientativo, que puede ser 2 y en la segunda la fórmula =B35-D23. Al introducir esta fórmula ya te será imposible calcular el valor de D23 mediante búsqueda del valor destino, pero por tanteo puedes lograr una aproximación a 1,74 W en el primer trozo y 1,07 W en el segundo.
