Herramienta Solver
Problemas de optimización
La herramienta Solver nos permite optimizar el valor de una celda, a la que llamaremos Objetivo, que depende linealmente de las celdas de un rango determinado, el cual puede estar sometido a restricciones. Como se ve, es en realidad el problema matemático de Programación Lineal.
Su funcionamiento se puede estudiar con un ejemplo:
Después de vender una casa, a una persona le quedan 170.000 € para invertir. Desea una inversión conservadora, por lo que duda entre varias inversiones
A) Depósito en banca de Internet, que está dando el 4,2% TAE, pero es un producto novedoso que no le termina de convencer
B) Su banco de toda la vida le ofrece plazo fijo con interés de 3,75% TAE, y que ella considera seguros.
C) Un producto vinculado a un fondo, con rendimientos del 6% pero sujeto a volatilidad.
En vista de la situación, decide invertir en B) al menos la mitad del capital, y en C) menos de 15.000 €
¿Qué cesta de inversiones le daría el máximo rendimiento?
Volcamos los datos en la tabla siguiente:
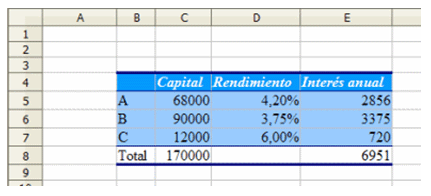
En la columna C hemos concretado unos capitales inventados, pero cercanos a la posible solución y con suma 170000. Sobre esta tabla podemos concretar los parámetros del problema:
Celda objetivo: E8, que es el rendimiento total.
Celdas que cambian: C5 a C7, la composición de la cesta.
Restricciones: C6 ha de valer, como mínimo, 170000/2 = 85000 €, la celda C7 no debe llegar a 15000 €, y la C8 ha de contener 170000 €
Objetivo que se pretende: Maximizar
Todo esto se puede concretar en la herramienta Solver.
Pulsa sobre el menú Herramientas y elige Solver...
En la ventana que se abre concreta objetivo, celdas que cambian, restricciones, etc.
Estudia bien la forma de hacerlo:
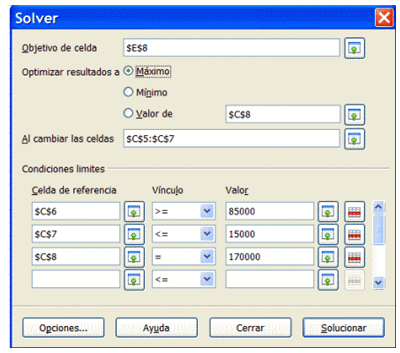
Pulsamos Solucionar, y en este caso existe la solución, 7027,50 €. Elegimos Mantener resultados y podemos ver que la solución es:

Invertir 70000 € en A, 85000 € en B y 15000 € en C
Otras posibilidades serían:
Pide Mínimo en lugar de Máximo y obtendrás la solución de 6375 €, si se invierte todo el dinero en C)
Puedes también lograr que la inversión rinda una cantidad determinada (entre el mínimo y el máximo), por ejemplo 6800 €. Para ello elige Valor de e iguálalo a 6800. Obtendrás una solución si en Opciones (busca el botón) no obligas a que los valores sean enteros: Obtendrás esta solución:
|
Capital |
Rendimiento |
Interés anual |
A |
19444,44 |
4,20% |
816,67 |
B |
135555,56 |
3,75% |
5083,33 |
C |
15000 |
6,00% |
900 |
Total |
170000 |
|
6800 |
Opciones de Solver
A veces Solver no puede encontrar la solución. Este se puede deber a tres causas:- El problema es de tipo indefinido. Existen muchas soluciones.
- Las soluciones tienden a infinito (especialmente en problemas de máximos) y se produce un desbordamiento.
- No hay convergencia. Las soluciones no se acercan lo suficiente al objetivo
Esta última posibilidad se puede a veces corregir con un botón de Opciones. Observa la ventana:
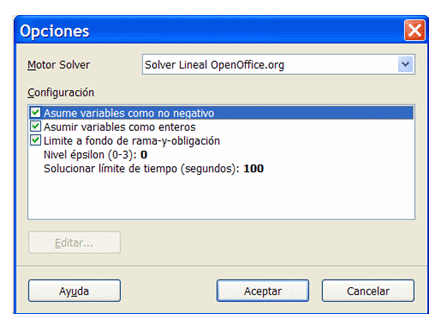
Tiene cuatro posibilidades de toma de decisión:
Asume variables como no negativo
Lo normal en problemas prácticos es que las cantidades sean positivas, luego esta opción debe estar activada siempre, salvo que admitas valores negativos, que quizás sean los que te devuelvan una solución.Asumir variables como enteros
Esta opción la marca claramente el problema. Hay variables, como las personas, los camiones o el número de llamadas telefónicas, que son números enteros, y otras, como el dinero o los porcentajes, que admiten decimales. En este caso deberás desactivar esta opción.Nivel épsilon
Pulsa con doble clic sobre esta opción para cambiar el nivel de exigencia de aproximación (el cero) a otros que toleren un error mayor (de 1 a 3)Límite de tiempo
Con 100 segundos tienes de sobra en ejemplos sencillos. Si ves que no converge de ninguna forma, amplíalo. En las Sugerencias de uso puedes consultar algún ejemplo más.
