Práctica: Errores en medidas repetidas
Como práctica de Estadística reproducirás los cálculos posteriores a una serie de medidas repetidas de una misma magnitud, procedimiento muy usado para estimar la medida verdadera y, en lo posible, su incertidumbre. Construirás un modelo que admita los resultados de las medidas y efectúe estimaciones sobre ellas.
Existen muchos métodos aproximados para estimar el error en una serie de medidas. Aunque la estimación de la medida verdadera se suele efectuar a partir de la media, en el cálculo de la incertidumbre de una medida se pueden usar diversos estadísticos, como la desviación media, la desviación estándar, el error típico, etc. Nosotros usaremos este último, que es el que mejor clasifica, a posteriori, las distintas medidas como fiables o desechables.
Comienza la práctica diseñando todos los textos y la estructura de las tablas de datos. Puede ser el de la imagen que sigue, pero cámbialo si tienes otras preferencias, o si usas ya otro esquema en trabajos de laboratorio. También puedes sustituir el error típico por otra medida que suelas usar. No escribas los símbolos O, X, y XX, que eso vendrá después. Por ahora escribe solo algunos datos, preferiblemente los mismos que figuran en la imagen de abajo.
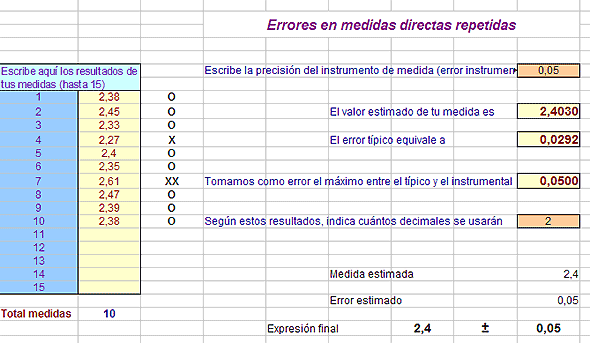
En la imagen se ve que se podrán admitir hasta 15 medidas, cantidad que quizás sea un poco excesiva. La zona en la que escribirás esas medidas es la de color amarillo. Selecciónala completa, y dale el nombre de medidas. Recuerda que basta con que pidas Insertar > Nombres > Definir y en el marco correspondiente escribes medidas y pulsas Aceptar.
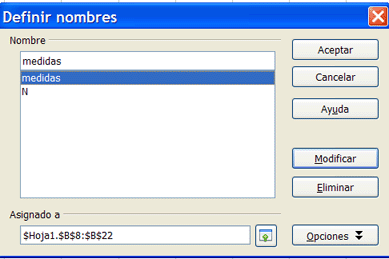
A partir de aquí te limitarás a rellenar fórmulas y más datos.
Total medidas: Basta que uses la fórmula =CONTAR(medidas). En el ejemplo son 11. Puedes situar el total debajo de la tabla.
Dale a ese total el nombre de N, por el procedimiento explicado en el párrafo anterior.
Error instrumental: Ese dato lo escribirás directamente, según la precisión que tenga el instrumento de medida. En la imagen es 0,05
Valor estimado: Hemos indicado que se suele usar la media de los datos, luego escribe la fórmula =PROMEDIO(medidas). En el ejemplo da el resultado de 2,3927
Error típico: Usaremos el error del muestreo, que equivale a la desviación estándar de la muestra (conjunto de medidas) dividida entre la raíz cuadrada de su número, luego la fórmula adecuada será =DESVEST(medidas)/RAÍZ(N). Si has usado los datos del ejemplo obtendrás 0,0283
Error máximo: Se suele elegir como error definitivo el máximo entre el error que nos da la Estadística y la precisión del instrumento. Por tanto, la fórmula adecuada será =MÁX(I6;I11) (suponiendo que fueran esas las celdas. Tú deberás usar, en lugar de I6 e I11, las referencias de las celdas en las que tengas los dos errores)
Decimales: A la vista del error, deberás elegir cuántas cifras significativas se usarán. En este modelo sólo se ajustan los decimales. Si el error es mayor que 1, no funcionará y deberás escribir tú lo que sigue.
En la imagen figuran dos decimales, para adaptarse a la primera cifra significativa del error de 0,05.
Medida estimada y error estimado: Ambas celdas usan la función REDONDEAR. Para escribir la media redondeada escribirás esta fórmula
=REDONDEAR("Celda en la que esté la media";"Celda en la que estén los decimales")
Sustituye la celda de la media por la referencia que tenga en tu modelo, y haz lo mismo con la celda de los decimales.
Para redondear el error debes utilizar también REDONDEAR.
Te dejamos como ejercicio la expresión final. Deberás usar el signo = para copiar los dos últimos datos en otra celda.
Para el ± usa la orden Insertar > Símbolos...
Distinción entre medidas aceptables y rechazables (opcional): Si la Estadística no es lo tuyo, olvida lo que sigue. Si te apetece intentarlo, lo puedes hacer así:
Si la distribución de errores siguiera la distribución normal (aproximadamente es así. Gauss descubrió su campana estudiando errores), el porcentaje de las medidas que se separa más de dos veces el error, sólo sería de un 4%, y de las que se separan más de 3, prácticamente es cero.
Podríamos aprovechar esto para clasificar las medidas en:
Aceptables: Si se desvían menos que el error multiplicado por 2. Las rotulamos con O
Sospechosas: Si su desviación está entre 2 y 3. Las marcamos con X
Rechazables: El resto de medidas, a las que marcaremos con XX. Estas medidas se deberían borrar y volver a calcular todo. En una hoja de cálculo, con su capacidad de recalcular, esta operación es instantánea.
Esta clasificación es convencional, y sólo nos servirá para destacar las medidas poco fiables. No tienes que seguirla al pie de la letra.
Para conseguir que a la derecha de cada medida aparezca el O, la X o la XX, podrás usar esta fórmula:
=SI(ESNÚMERO(B8);SI(ABS(B8-I$9)<2*I$14;"O";SI(ABS(B8-I$9)<3*I$14;"X";"XX"));" ")
Adáptala a tu modelo. En ella B8 es cualquier medida, por ejemplo la primera. I$9 la media (protegida por $ para poder arrastrar fórmulas hacia abajo), y I$14 el error típico.
Consiste en tres funciones SI anidadas. En la primera nos preguntamos si la celda B8 es un número, porque puede estar vacía. En caso afirmativo nos preguntamos si su distancia a la media es menor que dos errores típicos, con lo que la calificamos con un "O". Por último, si está a más de 3 errores le asignamos "XX" y si cae entre 2 y 3, la "X".
