Práctica: Análisis elementales de datos
El aprender a analizar datos nos llevaría a todo un curso nuevo, aparte de que a veces vale más la experiencia que las teorías que podamos estudiar. Incluimos aquí algunos consejos muy sencillos para que tus alumnos y alumnas puedan organizar pequeños análisis sobre sus datos con OpenOffice.org Calc.
Los desarrollaremos a partir de la siguiente tabla, que corresponde a las bajas por enfermedad que se han producido en tres supermercados de la misma empresa a lo largo del año.
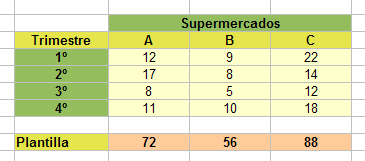
Inspección preliminar
Se debe estudiar el conjunto de datos en sí mismo, tomando nota previa al estudio, para encaminar este hacia las hipótesis que hallamos formulado, admitiendo las sorpresas que se puedan producir.
En este caso vemos que hay menos bajas en verano y que entre los otros primeros trimestres no hay mucha diferencia. También se observa que las bajas son ligeramente proporcionales a las plantillas.
Piensa tú si se te ocurren más observaciones.
Sumas por filas y columnas
La primera operación que se puede proponer en una tabla como esta es la de sumar por filas o por columnas, mediante la Autosuma o la función SUMA. Observa como se ha hecho en el modelo super.ods que contiene la tabla ejemplo y todas las transformaciones que se le vayan haciendo.
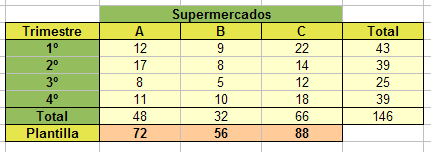
Como ves, con estas sumas tu alumnado puede darse cuenta de varios hechos muy importantes. En este ejemplo podrían ver:
- Qué supermercado ha tenido más bajas, discutiendo su significado respecto a la plantilla
- En qué trimestre se producen más bajas. Discusión sobre las estaciones del año y las vacaciones.
- Volumen total de bajas y su comparación con el total de las tres plantillas.
Estas distribuciones totales o marginales son la base de muchos gráficos posibles. Insertamos algunos como ejemplo. Intenta reproducirlos. Recuerda que para seleccionar columnas o filas disjuntas debes usar la tecla Ctrl mientras las seleccionas.
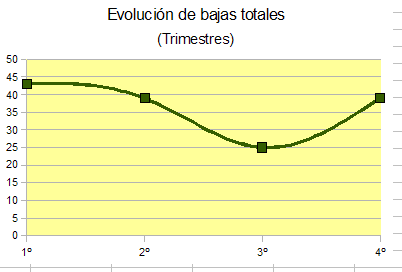
Se aprecia claramente la bajada que sufren en el tercer trimestre.
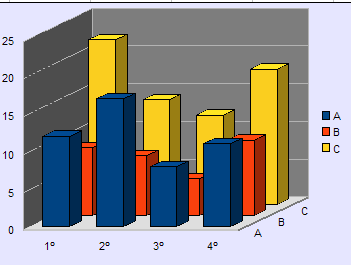
En este otro gráfico se percibe el conjunto total de la tabla, la distribución por trimestres y por centros, pero no permite la comparación directa. Sería más útil un gráfico de porcentajes.
Porcentajes respecto a los totales. Medidas relativas.
Si deseamos conocer en qué supermercado se falta más, no nos valen los datos puros, porque las plantillas son distintas. Deberemos calcular el porcentaje de cada dato respecto a la plantilla. Se usan los porcentajes para poder comparar datos pertenecientes a conjuntos de diferente procedencia, magnitud o naturaleza.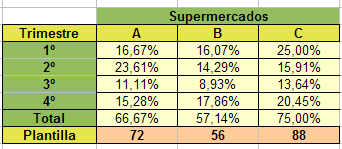
Los porcentajes se han obtenido dividiendo cada número de bajas entre la plantilla del supermercado, pasando después a formato de porcentaje.
En la figura puedes ver los resultados: en el supermercado en el que había más personal también se falta más en términos relativos. Quizás el tener que controlar a más personas permita alguna picaresca. De todas formas, las diferencias son muy pequeñas. En el segundo trimestre destaca el porcentaje de A. Intenta tú reproducir los cálculos y analizar más detalles.
Lo importante es que gracias a los porcentajes se pueden comparar
conjuntos de distinto tamaño o naturaleza.
También podemos hallar los porcentajes de cada trimestre respecto al total de bajas, para ver la intensidad de este fenómeno en cada caso. No des más importancia de la que tienen a estos porcentajes, porque como una misma persona puede faltar muchas veces, las sumas no cuadran, y sólo son indicadores.
Medias ponderadas
El sumar porcentajes por columnas tiene sentido (aunque no mucho) para ver el porcentaje total a lo largo del año, incluso si dividimos entre 4 nos resultaría la media anual por supermercado. Sin embargo, para calcular el porcentaje medio por trimestre no podemos sumar porcentajes, ni tampoco calcularles el promedio, porque corresponden a plantillas distintas y no son comparables directamente. En estos casos se debe explicar al alumnado que hay que conceder pesos a cada porcentaje según su plantilla.
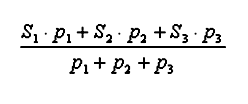
Usaríamos una media ponderada:
En la figura y en el modelo super.ods puedes ver los cálculos.
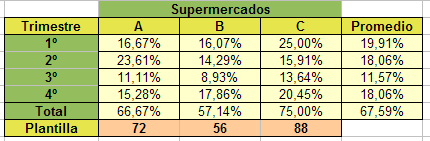
La última columna contiene la media. De esta forma se ve muy bien que sólo el tercer trimestre registra una disminución significativa de bajas y el primero un ligero incremento. Estudia las fórmulas que se han usado para calcular las medias.
Ahora el gráfico tridimensional tiene más sentido:
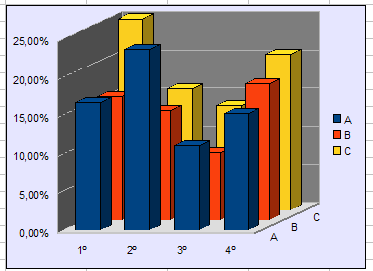
En este nuevo gráfico se perciben menos diferencias entre centros, porque al usar porcentajes se elimina el factor plantilla.
Estas comparaciones entre trimestres se pueden destacar mejor con la ayuda de los números índices.
Números índices
Si asignamos el valor 1 (o el 100%) a uno de los datos, por ejemplo al tercer promedio de la última columna), podríamos saber qué valor proporcional le correspondería a cada uno de los demás datos. De esta forma, si a uno le corresponde 106%, ya sabremos que es un 6% superior al otro. A esta cantidad la llamamos índice del segundo dato respecto al primero. En la Hoja de Cálculo basta dividir uno entre otro y darle formato de porcentaje.
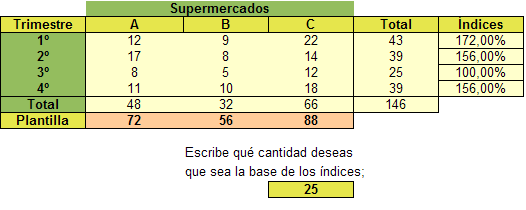
En la figura observarás que puedes escribir la cantidad que hará de base de los índices para que a partir de ella se calculen todos. Consúltalo en super.ods.
Si tomamos como base el cuarto trimestre, el primero le sobrepasa en un 10%, el segundo tiene un nivel prácticamente igual y el tercero baja a su 64,1%. Hemos desprendido al estudio de toda anécdota y nos hemos quedado con cuatro números que se comparan mediante sus porcentajes mutuos.Tratamiento estadístico
A estas sencillas operaciones de sumas, cocientes, porcentajes e índices se le puede añadir todo el conjunto de estudios estadísticos que permite una tabla bidimensional. Destacamos algunas operaciones:
Cálculo de medias, varianzas y desviaciones típicas, tanto por filas como por columnas.
Estudio del coeficiente de correlación entre dos filas o dos columnas concretas.
Pruebas de independencia y ajuste, ANOVA, etc.
Dejamos estas posibilidades como sugerencias.
